1. You are building a MODFLOW model of a regional aquifer system. As with any modeling scenario, you must make some simplifying assumptions and you decide to use a single model layer to represent an aquifer that consists of three hydrogeologic units with similar, but different hydraulic conductivity values. Accordingly, you will need to assign a reprsentative vertical and horizontal hydraulic conductivity for each grid cell in the model layer where the values you assign account for the effect of the three subunits. The thicknesses of the three subunits varies by location, but at the point you currently analzying, the parameters are as follows (from top to bottom):
Thompson formation: Thickness=30 ft, Kh=2 ft/d
Bower formation: Thickness=15 ft, Kh = 6.5 ft/d
Cascade formation: Thickess=60 ft, Kh = 1 ft/d
Assume that Kh/Kv = ~5. Calculate the horizontal and vertical K values you would assign to the cells in this region of the model.
2. For the situation described in the previous problem, assume that the total hydraulic head above the Thompson formation is 374.6 ft and just below the Cascade formation, the head is 382.4 ft. The elevation at the top of the Thompson formation is 369.8 ft.
a) Calculate the head loss through each of three units.
b) Calculate the total head at the center of each of the three units.
c) Suppose you inserted a piezometer in the middle of the Bower formation. How far above the piezometer screen would the water rise in the piezometer tube?
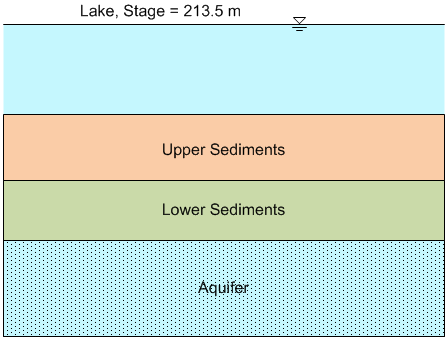
3. A lake is underlain by a large confined aquifer as shown below. The stage in the lake averages about 213.5 m and the average head in the aquifer is 197.3 m. The area of the lake is 6 km2. Between the lake and the aquifer there are two distinct sediment layers, each of which is about 6 m thick.

A water balance study on the lake shows that the difference between the inflow and outflow of the lake is 2000 m3/d. About 30% of this is thought to be as a result of evaporation. The rest is assumed to be lost to drainage through the bottom of the lake.
a. What is the combined (equivalent) vertical hydraulic conductivity of the two sediment layers? [m/d]
b. Assuming that the hydraulic conductivity of the lower sediments is 0.0004 m/d, what is the hydraulic conductivity of the upper sediments? [m/d]
c. Using the K values from part b, what percentage of the total head loss occurs in the lower sediments?
d. Assuming an effective porosity of 0.35 for the upper sediments and 0.25 for the lower sediments, what is the average travel time for a conservative tracer (non-sorbing) to move from the lake to the aquifer?
Do your calculations in Excel or Google Sheets. Show as much of your work as you can. If you use Google Sheets, download your solution as an Excel (*.xlsx) file. Upload your solution via Learning Suite.